RCM: On-Condition Task Interval Determination

Written by Gary West

The P-F curve shows the time interval between when a failure-in-the-making can be identified (potential failure, P) and the actual failed state where acceptable performance standards are no longer sustained (functional failure, F). This P-F interval is also known as:

• The warning period
• The lead time to failure
• The failure development period

Depending on the failure mode, this can vary from fractions of a second to many years.

How the P-F curve helps you identify failures

By conducting asset condition inspections on a scheduled basis, we can identify indicators of approaching failure before the asset breaks down. The P-F interval is used to determine how often these on-condition tasks must be performed. In order to detect the potential failure before it becomes a functional failure, the task frequency must be less than the P-F interval.

Conventional RCM wisdom suggests that it is usually sufficient to select a task periodicity equal to one-half the P-F interval. This ensures that the inspector detects the potential failure, while normally providing a reasonable amount of time (because the P-F interval is long enough to do something about it) to prevent the failure from occurring.

In order for the one-half P-F interval task periodicity to make any sense, you must suppose that the inspection to detect the potential failure is nearly 100 percent effective.

This presumption conceivably places the owner of an asset at significant risk, particularly when:

• The functional failure presents a significant risk to the organization because of safety, environmental, or significant operational consequences.
• The specific on-condition task may not identify the onset of failure with a sufficiently high degree of confidence because of some uncertainty or inconsistency of the inspection method.

RCM categorizes on-condition task techniques as follows:

• Condition monitoring techniques, which involve the use of specialized equipment to monitor the condition of other equipment
• Techniques based on variations in product quality
• Primary effects monitoring techniques, which entail the intelligent use of existing instruments and process monitoring equipment
• Inspection techniques based on the human senses.

The last two techniques, in particular, lend themselves to some subjectivity or uncertainty with the inspection results. Naval Air Systems Command has an RCM program for its in-service aircraft and support equipment. Its Guidelines for the Naval Aviation Reliability-Centered Maintenance Process, NAVAIR 00-25-403, discusses the use of equations to mitigate risk for on-condition tasks associated with high consequence failures (for example, safety and environmental). The NAVAIR equations are based on the premise that, in many cases, any attempt to identify a condition predicting a functional failure will not be 100 percent effective. These equations result in assigning on-condition task intervals with some number of inspections over the P-F interval, specifically to reduce the probability of failure to an acceptable level (P_acc) by taking into account the subjectivity or uncertainty with the inspection outcomes.

Figure 1 illustrates the relationship between P_acc and the probability of detecting the potential failure condition (ϴ) in calculating the appropriate number of inspections (n) in the P-F interval, using the NAVAIR equations. As you can see, the number of inspections required to mitigate the risk of failing to identify a potential failure condition can be quite significant (much greater than a single inspection at one-half the P-F interval) when the consequence of unforeseen failure is high.

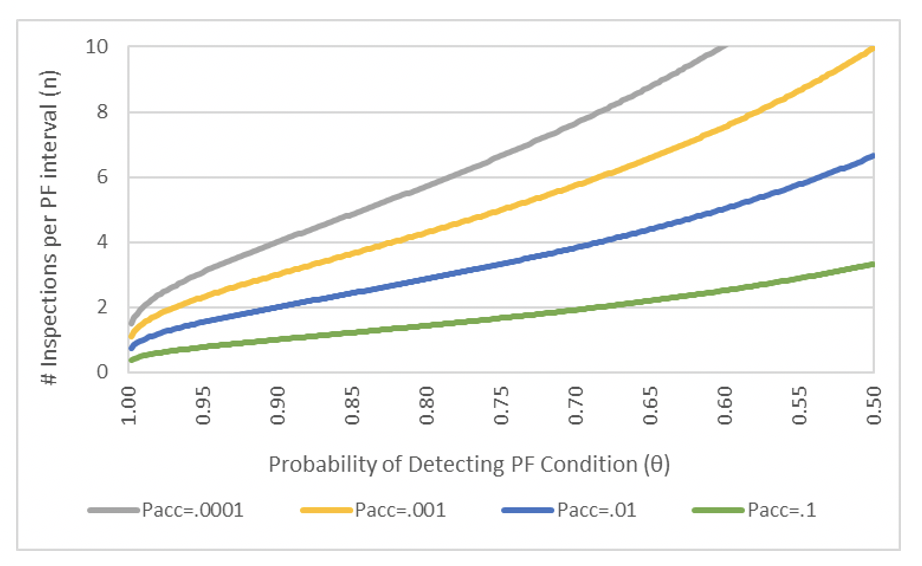
This notion of risk and on-condition task inspection uncertainty is probably not intuitive to most. For failures of high consequence, an on-condition task is only worth doing if it can be relied on (my emphasis) to give enough warning to ensure that action can be taken in time to avoid the actual failure. We could be placing the asset owner at significant risk by simply assigning the on-condition task periodicity at one-half the P-F interval, without considering uncertainty with the inspection results.

NAVAIR equations are of limited usefulness

I have concluded that the NAVAIR equations, themselves, are of limited usefulness. One problem is that ϴ can be a number that spans the continuum between just over zero (0%) to one (100%). Getting Review Group agreement for ϴ would likely be difficult, especially when ϴ can have such a weighty influence on the calculated number of required inspections per P-F interval (for example, when P_acc is 0.01 or less). For instance, a significant amount of Review Group time could be expended in trying reach agreement whether confidence in the inspection method is, say, 0.97, 0.92, 0.90, or 0.88.

NAVAIR’s RCM process does not recognize the concept of net P-F interval

A second problem is the task interval calculation equation itself. NAVAIR’s RCM process does not recognize the concept of net P-F interval. It appears that on-condition task inspections are performed when the aircraft is off-line, in a maintenance status. In the event the inspection reveals a potential failure condition, corrective action must be taken before the aircraft is placed back in service. The direct use of the NAVAIR equation I = (P-F)/n in the RCM2 and RCM3 processes does not make sense. For example, if n = 2, then the inspection periodicity would be one-half the P-F interval; but that also implies that two inspections would have to be accommodated within the P-F interval. For the worst case, the first inspection would be performed just before one-half the P-F interval and the second (if the potential failure was not identified at the time of the first inspection) just before functional failure; thereby, leaving the net P-F essentially zero. Nonetheless, the notion of risk that motivates use of the NAVAIR equations still remains relevant.

Fortunately, using the actual equations is unnecessary. Table 1 is a representation of the data used to populate the graph in Figure 1. Some of the data has been removed from the table for the sake of clarity.

Whenever it is established that the functional failure presents a sizable risk (say, P_acc is .01 or less), we could ask the Review Group, “Are you absolutely confident with the on-condition inspection method, fairly confident, or have some reservation?” The three categories of confidence (that is, absolutely confident, fairly confident, or some reservation) would correspond to ϴ = 0.99, 0.90, and 0.75 respectively. The data from the three, blue shaded rows in Table 1 could then be used to quickly determine the appropriate number of inspections per P-F interval.

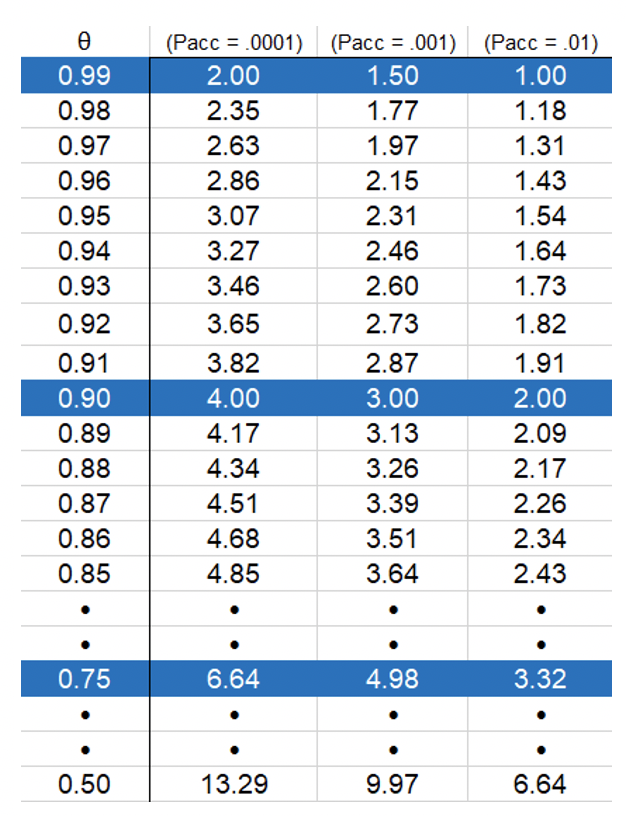
For example, the Review Group identifies a failure mode that presents a significant (or intolerable) risk to the organization. In order for the risk to be tolerable, the acceptable probability of occurrence (P_acc) might be 0.001 or less. (This method would work well in conjunction with an organization’s risk matrix.) The Group identifies an on-condition task, indicating they are fairly confident in the inspection method. With P_acc = .001 and ϴ = 0.90, Table 1 indicates three inspections in the P-F interval would need to be accommodated.

In order to accommodate the net P-F interval issue discussed above, one option would be to annotate on the Decision Worksheet that when a potential failure condition is identified, the asset must be immediately removed from service until corrective action is completed. A second option might be to subtract some kind of corrective action deferral time from the P-F interval before calculating the on-condition task interval, I = (P-F)/n. In either case, the Review Group would still have to determine if it is practical to perform the task at the proposed intervals.

High stakes failure modes require a risk-based approach

To detect a potential failure before it becomes a functional failure, the task frequency must be less than the P-F interval. For low-risk failure modes, a task periodicity equal to one-half of the P-F interval (or the net P-F interval) is entirely appropriate. However, the probability of potential failure detection can vary due to subjectivity or uncertainty with the inspection outcomes. Because any attempt to predict the onset of a functional failure cannot be 100 percent certain, high stakes failure modes (e.g., safety, environmental and even high impact operations consequences) require a risk-based approach in determining defensible on-condition task periodicities.

Gary West is owner of Targeted Maintenance Solutions and a U.S. Navy submarine veteran. For the past 36 years, he has worked in maintenance of reactor plants, facilities, and spent nuclear fuel handling equipment. He is a graduate of Oregon State University with a Bachelor of Science degree in Mechanical Engineering.